О тонкой структуре электоральных фальсификаций
Подбрасывание фальшивых бюллетеней к реальным имеет математическое ограничение на итоговый результат. Для более высоких результатов необходимо менять реальные бюллетени.
С декабря 2011 года стало доброй традицией вертеть данные российских выборов, разглядывая их статистические свойства. Простейший анализ такого рода это построение результатов каждого избирательного участка (УИКа) на осях «Явка»—«Результат кандитата/партии». При честном подсчёте голосов результат практически не зависит от явки, а подбрасывание к реальным голосам дополнительных (фальшивых) бюллетеней за определённую партию/кандитата приводит к одновременному увеличению и явки, и результата этой партии/кандитата, а следовательно, к ярко выраженной статистической корреляции между результатом и явкой. Проявление этих корреляций на графике «Явка»—«Результат» вы можете поразглядывать сами в Лаборатории Электоральной Статистики для данных самых разных выборов. Здесь для иллюстрации я приведу такой график для официальных данных парламентских выборов 2021 года, построенный Сергеем Шпилькиным (источник):
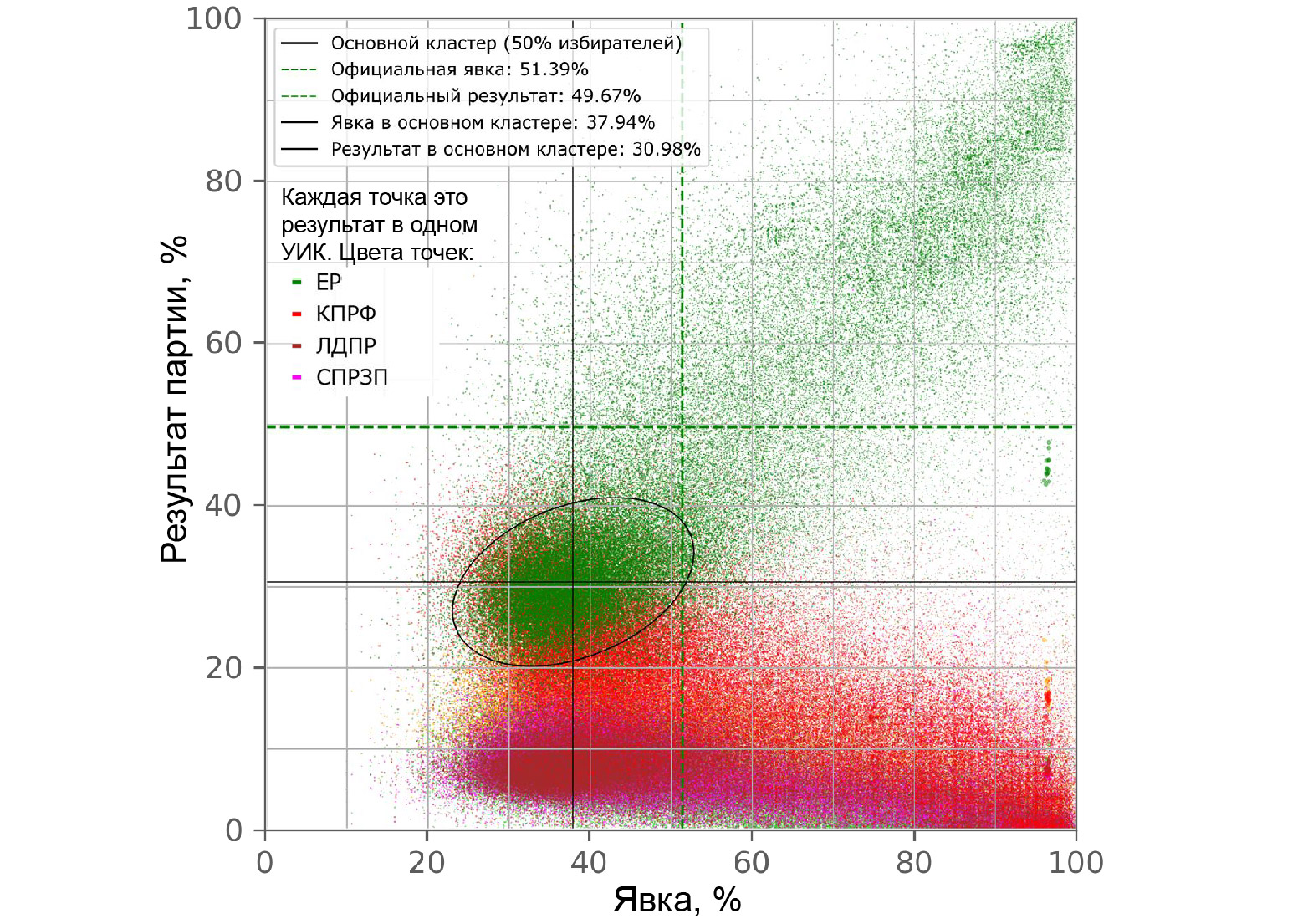
Помеченный здесь «основной кластер» наиболее похож но то, как обычно выглядят честные выборы (примеры смотрите тут). «Хвост кометы», уходящий вправо и вверх от основного кластера — это классическое последствие выборных фальсификаций.
Давайте зададимся вопросом: как сместится точка из основного кластера, если оставить её реальные голоса без изменений, но подбросить к ним дополнительные голоса «за»?
Пусть исходная точка (УИК) имела явку x0 и результат y0. Значит, «за» проголосовала доля x0y0 от общего числа зарегистрированных избирателей. Пусть число подброшенных (фальшивых) голосов «за» составляет долю v от общего числа зарегистрированных избирателей. Другими словами, после вброса явка возрастёт на v и станет равна (x0 + v). Поскольку новая явка не может быть выше единицы (100%), это ограничивает максимальный размер вброса: v ≤ (1 − x0).
Результат целевой партии, изначально равнявшийся y0, после вброса станет равен
Вот иллюстрация того, как ведёт себя эта формула для нескольких стартовых точек (x0, y0) и различных v.
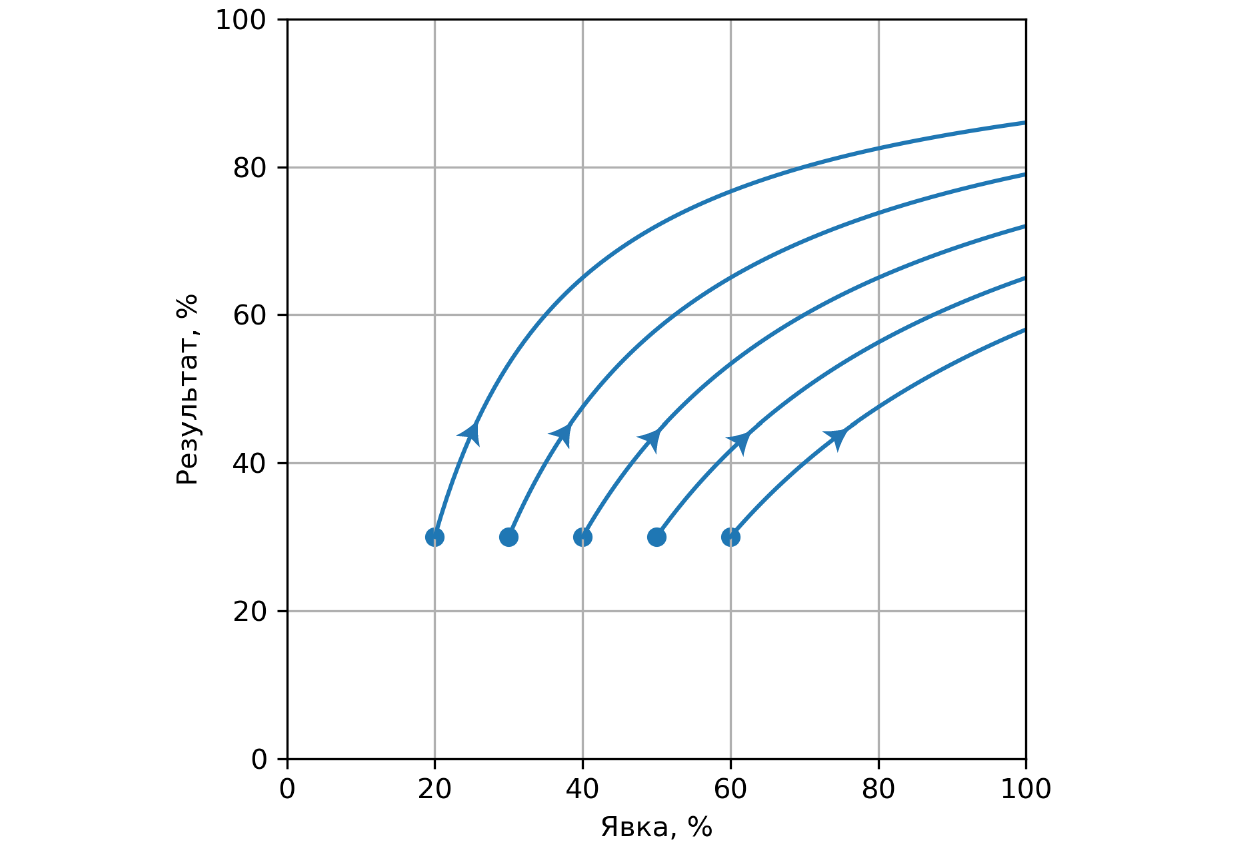
Можно заметить, что после вброса нельзя достичь результата выше, чем (1 − x0 + x0y0) при максимально возможном вбросе v = (1 − x0). Именно в эти максимумы утыкаются своими правыми краями кривые на графике выше.
Дальше я построил такие же кривые (применяя формулу выше), стартующие из всех точек внутри основного кластера «Единой России». Получившийся пучок кривых образует зону, которую я пометил жёлтым цветом поверх графика Сергея Шпилькина:
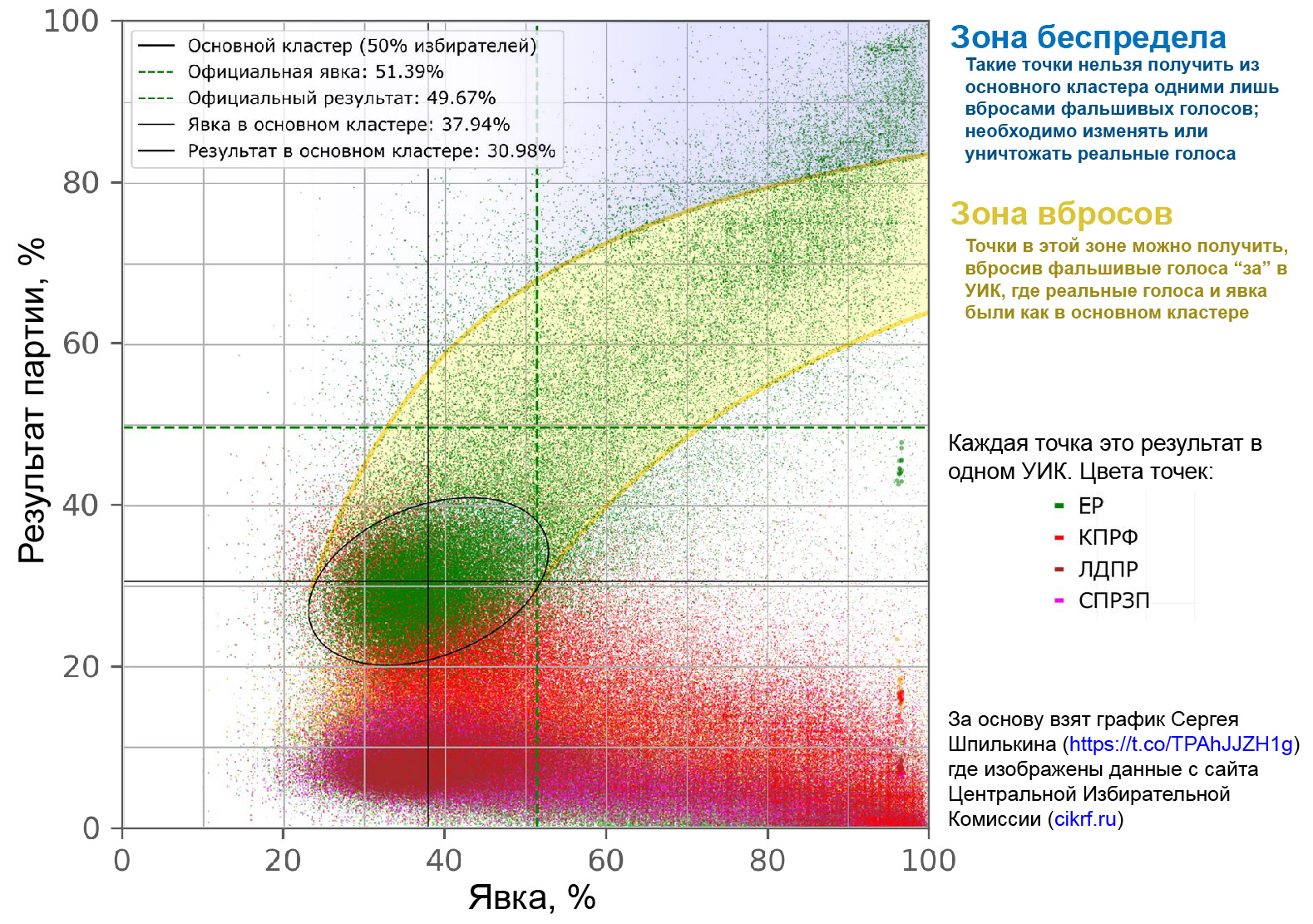
УИКи внутри жёлтой зоны для достижения своего результата могли ограничиться лишь вбросами фальшивых голосов, но УИКам выше жёлтой зоны было необходимо менять или уничтожать реальные голоса (верхний правый угол, синяя «Зона беспредела»).